关于e的负x平方的积分

Author: [GGGGWHW]

Link: [https://zhuanlan.zhihu.com/p/651305078?utm_id=0]

简介

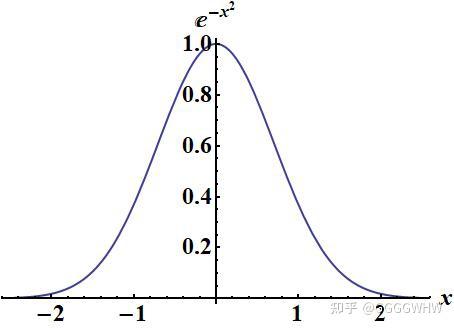
在统计学和物理学中经常要对形如 $f(x)=e^{-x^2}$ 这样的函数进行积分, 相当于求上图中函数曲线与 $x$ 轴之间所夹的面积. 本文将展示该函数和类似函数的积分过程.

考虑幂级数展开

考虑到 $F(x)=\int e^{-x^2}\mathrm{d}x$ 并不能得到一个简单的函数表达式, 所以不妨将被积函数先根据泰勒公式展开.

$$\begin{aligned} & \because e^x=\sum_{n=0}^{+\infty}\frac{x^n}{n!} \& \therefore e^{-x^2}=\sum_{n=0}^{+\infty}\frac{(-x^2)^n}{n!}= \sum_{n=0}^{+\infty}\frac{(-1)^nx^{2n}}{n!} \&\therefore F(x)=\int e^{-x^2}\mathrm{d}x = \sum_{n=0}^{+\infty}\int \frac{(-1)^nx^{2n}}{n!}\mathrm{d}x = \sum_{n=0}^{+\infty} \frac{(-1)^nx^{2n+1}}{n!(2n+1)}+C \end{aligned}$$

令 $C=0$ , 即 $F(0)=0$ , 则 $F(x)= \sum_{n=0}^{+\infty} \frac{(-1)^nx^{2n+1}}{n!(2n+1)}$ . 这个幂级数的收敛半径是 $+\infty$ , 但是收敛速度随着 $x$ 的变大迅速变慢. 比如:

当 $x=1$ 时, $\sum_{n=0}^{8} \frac{(-1)^nx^{2n+1}}{n!(2n+1)}$和$F(x)$的误差为 $1.33\times10^{-7}$ .

当 $x=2$ 时, $\sum_{n=0}^{8} \frac{(-1)^nx^{2n+1}}{n!(2n+1)}$和$F(x)$的误差为 $0.0555$ .

当 $x=2$ 时, $\sum_{n=0}^{17} \frac{(-1)^nx^{2n+1}}{n!(2n+1)}$和$F(x)$的误差为 $4.83\times10^{-7}$ .

当 $x=3$ 时, $\sum_{n=0}^{17} \frac{(-1)^nx^{2n+1}}{n!(2n+1)}$和$F(x)$的误差为 $1.305$ .

当 $x=3$ 时, $\sum_{n=0}^{26} \frac{(-1)^nx^{2n+1}}{n!(2n+1)}$和$F(x)$的误差为 $2.219\times10^{-4}$ .

所以这个幂级数对于求积分上限为较大数字的定积分不是很实用, 还不如直接通过分割被积函数, 然后进行数值积分方便.

考虑函数对称性

虽然不知道 $F(x)$ 的简单表达式, 但是不影响我们求一个特殊的定积分: $\int_{-\infty} ^{+\infty}e^{-x^2}\mathrm{d}x$ .

考虑到被积函数是一个偶函数,所以 $\int_{-\infty} ^{+\infty}e^{-x^2}\mathrm{d}x =2\int_{0} ^{+\infty}e^{-x^2}\mathrm{d}x$ .
变形后, 由于不能直接求被积函数的原函数 $F(x)$ , 所以上面的操作对于我们解决问题依然没有帮助.

考虑在高维空间解决

再换一个思路, 有理数域解决不了的问题, 放到实数域说不定就解决了; 实数域解决不了的问题, 放到复数域说不定就解决了. 同样地, 一元函数解决不了的问题, 换成二元函数说不定就解决了.

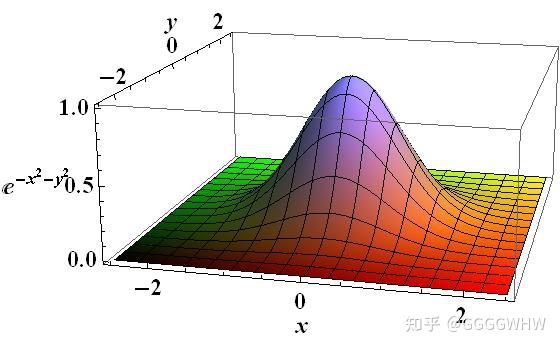
将文章开头的函数图像绕着纵轴旋转 $180°$ , 旋转过程中函数曲线在空间画出一个曲面, 如下图所示:

曲面的函数表达式为 $f(x,y)=e^{-x^2-y^2}$ 现在我们试着求上图中函数曲面与 $xOy$ 平面之间所夹的体积.

$$\begin{aligned}&\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}e^{-x^2-y^2}\mathrm{d}x\mathrm{d}y\=& \int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}e^{-x^2}\cdot e^{-y^2}\mathrm{d}x\mathrm{d}y\=& \int_{-\infty}^{+\infty}e^{-x^2}\mathrm{d}x\cdot\int_{-\infty}^{+\infty}e^{-y^2}\mathrm{d}y\=& (\int_{-\infty}^{+\infty}e^{-x^2}\mathrm{d}x)^2 \end{aligned}$$

惊喜地发现, 这个曲面积分结果恰好是我们要求的曲线积分的平方, 可是我们依然不知道这两个积分的结果.

考虑坐标变换解决

经验告诉我们, 对于轴对称图形, 柱坐标系比直角坐标系用起来会更方便一些.

坐标转换:

$\begin{cases} x=r\cdot\cos\theta\ y=r\cdot\sin\theta\ r=\sqrt{x^2+y^2}\ \mathrm{d}x\mathrm{d}y=r\mathrm{d}r\mathrm{d}\theta\ \end{cases}$

于是曲面积分

$$\begin{aligned} & \int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}e^{-x^2-y^2}\mathrm{d}x\mathrm{d}y\=& \int_{\theta=0}^{2\pi}\int_{r=0}^{+\infty}e^{-r^2}r\mathrm{d}r\mathrm{d}\theta\=& 2\pi\int_{r=0}^{+\infty}e^{-r^2}r\mathrm{d}r\=& \pi\int_{r^2=0}^{+\infty}e^{-r^2}\mathrm{d}(r^2)\=& -\pi\int_{-r^2=0}^{-\infty}e^{-r^2}\mathrm{d}(-r^2)\=& -\pi\int_{-r^2=0}^{-\infty}\mathrm{d}(e^{-r^2})\=& -\pi e^{-r^2}\mid_{-r^2=0}^{-\infty}\=& -\pi (e^{-\infty}-e^{0})\=& \pi \end{aligned}$$

之前已经证明曲面积分结果是曲线积分结果的平方, 所以

$$\begin{aligned}& \int_{-\infty} ^{+\infty}e^{-x^2}\mathrm{d}x=\sqrt\pi\& \int_{0} ^{+\infty}e^{-x^2}\mathrm{d}x=\frac12\int_{-\infty} ^{+\infty}e^{-x^2}\mathrm{d}x=\frac{\sqrt\pi}2\&\end{aligned}$$

结论

$$\begin{aligned} & \int_{-\infty} ^{+\infty}e^{-x^2}\mathrm{d}x=\sqrt\pi\& \int_{0} ^{+\infty}e^{-x^2}\mathrm{d}x=\frac{\sqrt\pi}2\&\end{aligned}$$

【习题】

习题1.

求 $\int_{-\infty} ^{+\infty}xe^{-x^2}\mathrm{d}x$ .

$$\begin{aligned} 解: & \int_{0} ^{+\infty}xe^{-x^2}\mathrm{d}x\=& \frac{1}{2}\int_{x^2=0} ^{+\infty}e^{-x^2}\mathrm{d}(x^2)\=& -\frac{1}{2}\int_{-x^2=0} ^{-\infty}e^{-x^2}\mathrm{d}(-x^2)\=& -\frac{1}{2}\int_{-x^2=0} ^{-\infty}\mathrm{d}(e^{-x^2})\=& -\frac{1}{2}e^{-x^2}\mid_{-x^2=0} ^{-\infty}\=& \frac{1}{2}\end{aligned}$$

习题2.

求 $\int_{-\infty} ^{+\infty}x^2e^{-x^2}\mathrm{d}x$.

$$\begin{aligned}解: & \int_{0} ^{+\infty}x^2e^{-x^2}\mathrm{d}x\=& \frac{1}{2}\int_{x=0} ^{+\infty}xe^{-x^2}\mathrm{d}(x^2)\=& -\frac{1}{2}\int_{x=0} ^{+\infty}xe^{-x^2}\mathrm{d}(-x^2)\=& -\frac{1}{2}\int_{x=0} ^{+\infty}x\mathrm{d}(e^{-x^2})\=& -\frac{1}{2}(xe^{-x^2}\mid_{x=0} ^{+\infty}-\int_{x=0} ^{+\infty}e^{-x^2}\mathrm{d}x)\=& \frac{1}{2}\int_{x=0} ^{+\infty}e^{-x^2}\mathrm{d}x\=& \frac{1}{2}\times\frac{\sqrt{\pi}}{2}\=& \frac{\sqrt{\pi}}{4}\end{aligned}$$

补充证明为什么 dxdy=rdrdθ？

直角坐标与极坐标的互化中，为什么 dxdy=rdrdθ？

Author: [予一人]

Link: [https://www.zhihu.com/question/368888687/answer/992671463]

这是一个好问题，而要真正理解这个问题，你首先需要在头脑里消除一种误会：

${\rm d}x{\rm d}y,{\rm d}r{\rm d}\theta$ 这样的记号并不代表通常意义上的乘法，因此不能按照通常的多项式乘法来处理。事实上，它们是所谓的楔形积（wedge product），相当于**外积。**严格来讲，这记号应该写作 ${\rm d}x\wedge{\rm d}y,{\rm d}r\wedge{\rm d}\theta.$

这种运算规定：

$a \wedge b=-(b \wedge a),~~~ a \wedge a=0\$ 于是

$\mathrm{d}r\wedge\mathrm{d}r=0,\quad \mathrm{d}\theta\wedge\mathrm{d}r=-(\mathrm{d}r\wedge\mathrm{d}\theta),\quad \mathrm{d}\theta\wedge\mathrm{d}\theta=0\$

于是
$$\begin{aligned}{\rm d}x\wedge{\rm d}y&={\rm d}(r\cos\theta)\wedge{\rm d}(r\sin\theta)\&=(-r\sin\theta{\rm d}\theta+\cos\theta{\rm d}r)\wedge(r\cos\theta{\rm d}\theta+\sin\theta{\rm d}r)\ &=-r\sin^2\theta ({\rm d}\theta \wedge{\rm d} r)+r\cos^2\theta ({\rm d}r \wedge{\rm d} \theta)\ &=r\sin^2\theta ({\rm d}r \wedge{\rm d} \theta)+r\cos^2\theta ({\rm d}r \wedge{\rm d} \theta)\ &=r(\sin^2 \theta+\cos^2 \theta) ({\rm d}r \wedge{\rm d} \theta)\ &=r({\rm d} r\wedge{\rm d} \theta)\\end{aligned}$$